#Graph
Conversational processes are based on a mathematical structure called Oriented Rooted Graph, or simply Graph.
Graph: definition
By definition, a Graph is defined by:
- a set of standard nodes, identified with the symbol🔵, and functional nodes, identified with the symbol 🔷;
- among all the nodes, one is identified as the unique root of the graph;
- a set of edges, identified by arrows that connect a node to another
Node: definition
A node is a unique state of the conversation. It's identified by:
- a mandatory unique Id, like
Q1, Q2, ..., F1, F2, ...Ids starting withQrefer to standard nodes, meanwhile ids starting withFrefer to functional nodes. Node Ids are assigned by the system and can't be modified by the user. - an optional variable name defined by the user which gives a semantic to the node.
For example, the node Id
Q1with text "What's your name?" may havefirstNameas variable name assigned. - a mandatory text in case of standard node, the function name in case of functional node. Note that a node may have up to 5 text boxes.
A node contains also other optional settings that can be configurated from the platform, like the speed of rolling out the messages or the deployment of the outgoing edges in case of buttons.
Edge: definition
An edge is a transition rule from a node to another. It's defined by:
- a mandatory source, which refers to a node Id
- a mandatory target, which refers to a node Id (it can be the same of the source, therefore we have a loop)
- a mandatory type of interaction (the user can choose between a button, a free-text box, a calendar and many more)
- a text, which is mandatory only for buttons.
- an optional key, which is an alternative value of the edge, useful to pass richer information to the system.
For example, the node "Is that an emergency?" has two outgoing edges: "Yes" with key
100and "No" with key0. The integrated claim platform may not know the meaning of "Yes" and "No", but the numbers100or0are correctly accepted as valid urgency indexes.
Depending on the type of interaction, there are various configuration settings that can be applied. For example, validation of the free-text (maximum number of characters, email-format, number validation), range of dates clickable on the calendar and many others.
Connecting nodes with edges
The conversational process transits from a node to another through an edge. In other words, the evolution of the conversation is given by
- the user in case of normal edge connections
- the custom logic in case of functional nodes
Two nodes can be easily connected by dragging and dropping a line on the graph, starting with the initial node and targeting the final node.

The transaction between two nodes will be represented by an arrow outgoing from the source state and incoming into the target node. Once created, the connection can be configured with a number of settings, depending of the desired experience to deliver to the end-user.
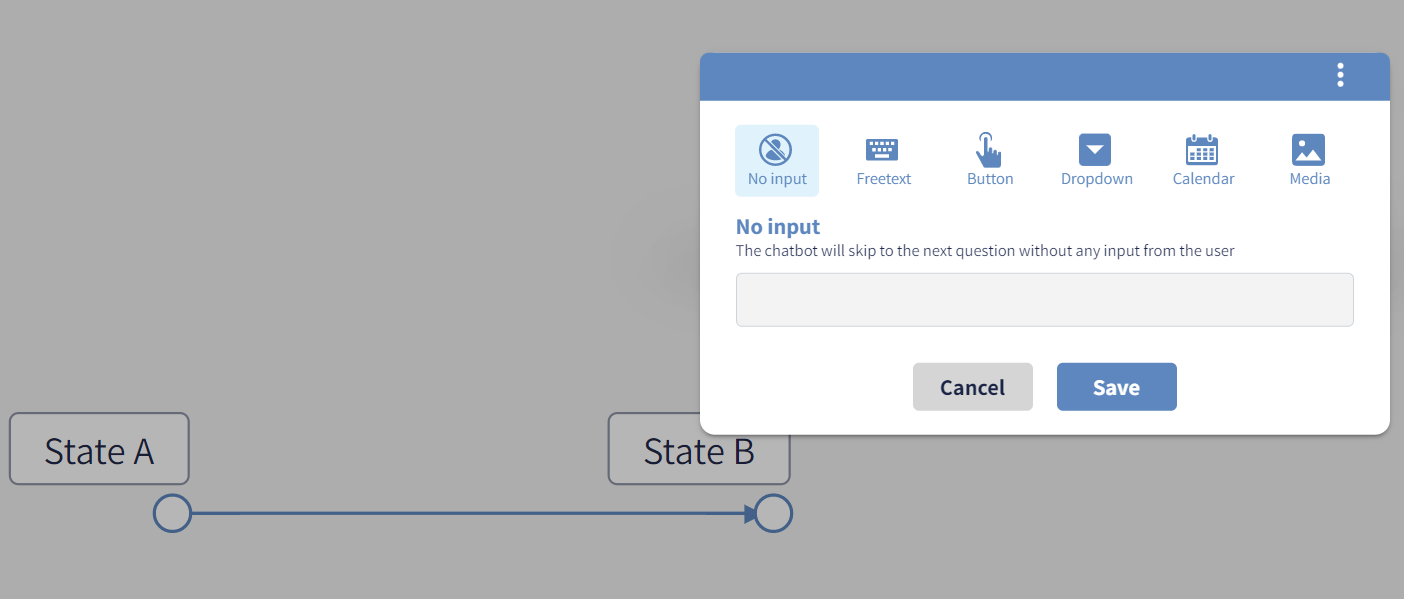
Concept of jump nodes
By definition, a Graph allows loops. This is true also for a conversational process. Let's consider following simple example of email validation:
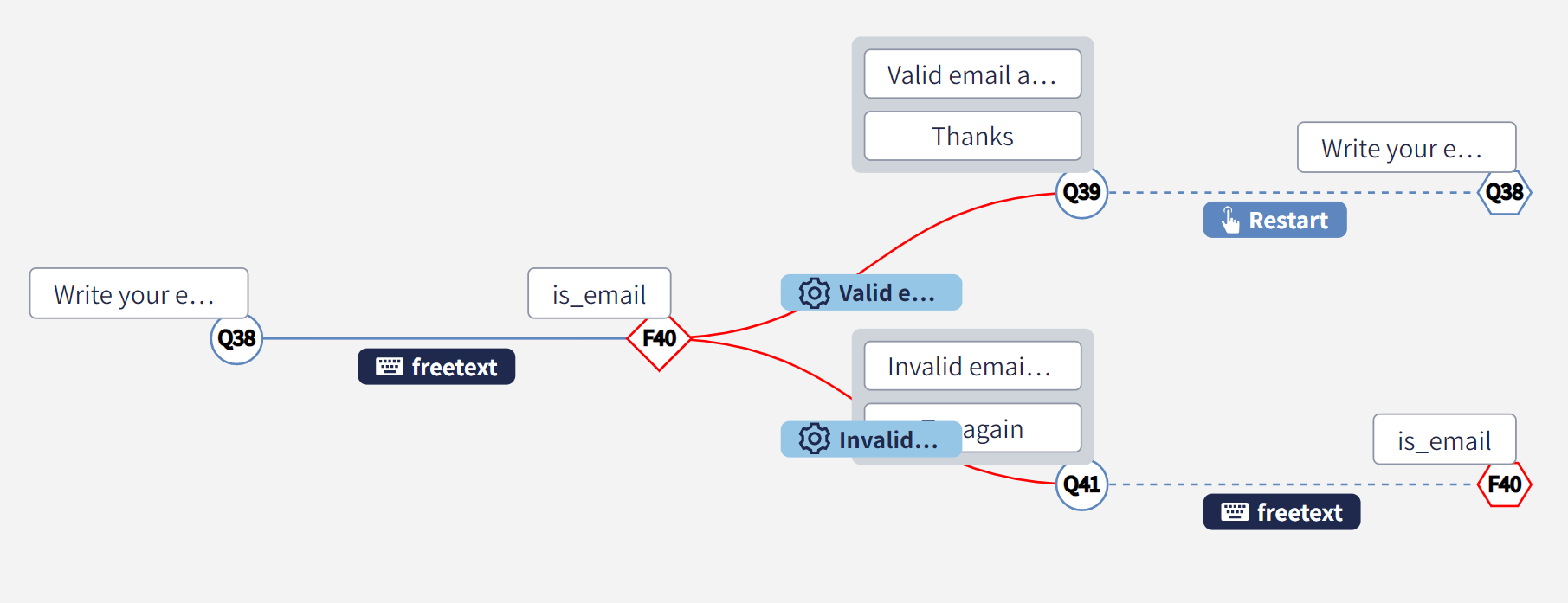
The process starts asking the end-user to type their email address, then it passes it to the is_email functional node which can return either valid or invalid.
In case of invalid email, the process would ask the end-user to try again and "go back" to execute another time the is_valid email.
Drawing loops may remove the ordering left-right and eventually decrease the readability of the Graph, therefore every time a node with at least one incoming edge is referred, a virtual jump node is created, linked with a dashed connection. In the way, the Graph is unfolded into a Tree, that is a Graph with no loops.
Jump nodes are represented with the ⬣ symbol: they merely refer to a real node and cannot be modified, but only deleted. The edge is dashed to remark that the connection is leading to a recursion in the logic.
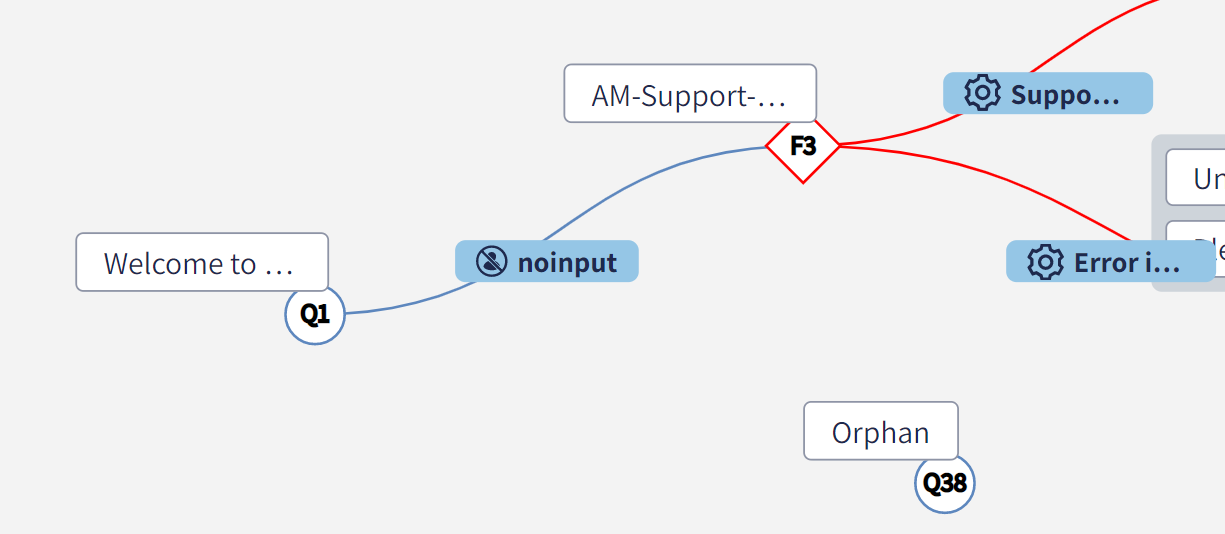
Concept of orphan nodes
An orphan node is a node not connected by any edge: they are like isolated nodes. The concept may be extended to subsets of the graph that are not reachable from the root. In order to minimize the maintenance of a conversational process, best practices suggest to avoid orphan nodes and unreachable nets.
Search function
Patterns are searched in the following assets:
- Node Ids
For example, the pattern
Q1will extract nodesQ1, Q10, Q11, ..., Q100, ... - Standard node variable
For example, the pattern
firstNamewill extract the nodeQ1which has variablefirstName - Standard node and edge textual content
For example, the pattern
Nowill extract the edges with textNo,Not this time,...and the nodes with textNothing is impossible,Which part of Normandy?,... - Functional node name
For example, the pattern
emailshould extract the standard nodeQ1with textWhat's your email?and the functional nodeF1with functionis_emailassigned.
The mathematical definition
The Graph Theory branch of the Theoretical Computer Science allows to craft a more compact definition of the graph.
A graph or conversational process G, is defined by:
G = <N, E ⊆ N x N, ns ∈ N>where:
- a set of unique states
N, named nodes, such as for eachn ∈ N:n = <id, variable name, text, metadata, type> - a set of unique connections
E ⊆ N x N, named edges, such as for eacheinE:e = <sourse ∈ N, target ∈ N, id, key, text, metadata>and the combination of the three elements
<source, target, id>is unique; - a node
ns ∈ Nis labelled as the root of the graph
For the nodes, only the id is mandatory and unique; the element variable name is optional, meanwhile text is mandatory only for standard nodes.
For the edges, the combination <source, target, id> must be unique.
The element text is mandatory only when id > 0, meanwhile key is always optional.
The element type is not strictly required for the logic of the conversational process, but it allows to unfold the loops and the cycles of the graph: in this way, the layout will be more similar to a tree, which is easier to understand and visualize.
Note that, despite a tree-style representation of the logic, the underlying mathematical structure of a conversational process is not a tree because trees do not have the same expression power of a graph and reduce drastically the flexibility of the process and the conversation as well.
Incidence of a node
The incidence of a given a node n ∈ N is the set of edges incoming into such node:
inc(n) = [e ∈ E | e.target = n]
In other words, inc(n) is the set of connections ending into the node n.
Let’s indicate |inc(n)| the number of elements of the set inc(n).
First Corollary
The First Corollary says that for each n ∈ N | inc(n) = 1,
e ∈ inc(n) has e.type = NIn other words, if a node n has only one incoming edge e, then e has type = N.
Second Corollary
The Second Corollary says that for each n ∈ N | |inc(n)| > 1 and n ≠ ns,
∃ I ⊂ inc(n) |
|I| = |inc(n)| - 1
and
∀ e ∈ I e.type = Dand
∃ e ∈ [inc(n) - I] | e.type = NFor example, if a node n has 10 incoming connections then all have type = D except one which has type = N.
Theorem of Graph unfolded
Given the combination of the two corollaries, for each n ∈ N | n ≠ ns,
∃! e ∈ inc(e) | e.type = NAll the other edges e ∈ inc(c) has e.type = D.
In the special case of the root ns, all the connections e ∈ inc(ns) have e.type = D.
Thanks to this theorem, the consistency of the graph is validated. Therefore, the graph can be unfolded into a tree by leveraging the jump nodes.
All the editing operations on the graph (add/remove a node, add/remove a connection, etc …) must comply with the theorem to preserve the consistency of the graph.
As a general rule, when a node n ∈ N has multiple incoming edges, the most recent has type = N and the others have type = D, if not already assigned otherwise.